|
|
Coordonnées barycentriques des pieds de céviennes
Notons (u,v,w) les coordonnées barycentriques d’un point P de 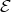 par rapport
au triangle Δ : on a u + v + w = 1 et
par rapport
au triangle Δ : on a u + v + w = 1 et
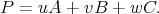
Les coordonnées barycentriques des pieds A′,B′,C′ des céviennes passant par P sont alors données par
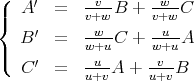 | (6) |
Il suffit de vérifier la première. Les autres seront vraies par symétrie. Le point A′ ainsi décrit appartient au segment [B,C] puisqu’il est combinaison affine de ses extrémitiés B et C. D’autre part, puisque
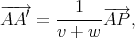
A′ appartient aussi à la cévienne AP.
Coordonnées barycentriques d’un orthocentre Déterminons à présent les coordonnées barycentriques de l’orthocentre H du triangle Δ relatif à un produit scalaire g.
Preuve. Pour les expressions (u,v,w) en termes des nombres p,q,r, on observe d’abord que u + v + w = 1. Ensuite, on vérifie directement que chaque cévienne passant par le point ayant les coordonnées (u,v,w) proposées est perpendiculaire au côté opposé au sommet dont elle est issue. Il suffit même de le vérifier pour deux, par exemple BB′ et CC′. En utilisant (1) et les relations (6), il vient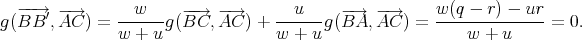
Ainsi, BB′⊥ AC. Vu la symétrie des expressions en p et q, on a alors automatiquement CC′⊥ AB.
Il reste à exprimer (u,v,w) au moyen des angles de Δ. On utilise pour cela les formules (2), (4) et (5). Illustrons le calcul dans le cas de u, les autres étant analogues :
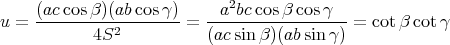
puisque 2S = ac sin β = ab sin γ. D’où la propriété.
Proposition 3.2 Le point P de coordonnées barycentriques (u,v,w) par rapport à Δ est un orthocentre de Δ si et seulement si P est un des sommets de Δ ou uvw > 0.
Proposition 3.3 Soit un produit scalaire g de
 .
Les positions relatives des orthocentres des triangles de (
.
Les positions relatives des orthocentres des triangles de ( ,g) sont décrites
par les coordonnées barycentriques (1, 0, 0), (0, 1, 0) et (0, 0, 1) correspondant
aux triangles rectangles, ainsi que par les coordonnées barycentriques (u,v,w)
vérifiant uvw > 0.
,g) sont décrites
par les coordonnées barycentriques (1, 0, 0), (0, 1, 0) et (0, 0, 1) correspondant
aux triangles rectangles, ainsi que par les coordonnées barycentriques (u,v,w)
vérifiant uvw > 0.
|
|
Preuve. (De 3.2.) Vu la Proposition 3.1, les coordonnées barycentriques d’un orthocentre de Δ vérifient uvw ≥ 0. De plus, ce produit est nul si et seulement si r = 0, q = r ou p = r, c’est-à-dire si et seulement si Δ est rectangle en A, B ou C respectivement. Inversement, si les coordonnées barycentriques (u,v,w) vérifient uvw > 0, alors il existe un produit scalaire g pour lequel
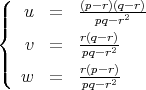
Ces relations impliquent en effet que
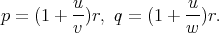
Les coordonnées (u,v,w) étant homogènes en p,q et r, ces derniers ne sont définis qu’à un multiple près (conformément au fait que la position relative de l’orthocentre est invariante par similitude). Les valeurs de p et q ci-dessus conviennent donc à condition de pouvoir choisir r pour que p,q,r vérifient les conditions p > 0 et pq - r2 > 0. Elles garantissent en effet que les formules (1) définissent un produit scalaire. La condition p > 0 détermine le signe de r, qui ne peut être nul. D’autre part, avec les valeurs de p et de q ci-dessus, on a
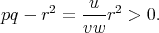
D’où la thèse.
Le lieu des orthocentres du triangle Δ est illustré à la figure 6. Pour rappel, en effet, les signes des coordonnées barycentriques sont distribués comme indiqués sur la figure 7.
Les point intérieurs au triangles correspondent aux orthocentres des triangles acutangles et les sommets de Δ aux triangles rectangles. Enfin, les autres positions sont relatives aux triangles ayant un angle obtus : Δ est obtus en A dans la région (+ --), etc.
Corollaire 3.4 Le lieu du centre des cercles circonscrits au triangle Δ est formé des milieux des côtés de Δ et des points de coordonnées barycentriques (u,v,w) vérifiant (1 - 2u)(1 - 2v)(1 - 2w) > 0.
Preuve. En effet, le centre de gravité de Δ est indépendant du produit scalaire. Il est par ailleurs le centre d’une homothétie, de rapport -1∕2, qui applique l’orthocentre sur le centre du cercle circonscrit. Elle applique aussi les sommets du triangle sur les milieux des côtés opposés. Si les coordonnées barycentriques de l’orthocentre sont (u,v,w), le centre O du cercle circonscrit s’écrit alors
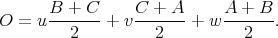
Ses coordonnées barycentriques sont donc ((v + w)∕2, (w + u)∕2, (u + v)∕2). La conclusion est aisée.
Où il est question du nombre d’or Rappelons que gX désigne le produit scalaire pour lequel un triangle donné est rectangle en son sommet X, les côtés issus de ce sommet étant de longueur 1.
L’ensemble des produits scalaires de
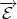 étant
convexe, nous obtenons une famille de produits scalaires en posant
étant
convexe, nous obtenons une famille de produits scalaires en posant
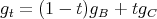
avec t 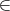 [0, 1]. Cette famille décrit le segment [gB,gC] contenu dans
[0, 1]. Cette famille décrit le segment [gB,gC] contenu dans
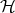 +(
+(
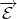 ).
Cependant, ce dernier étant ouvert, il contient un plus grand segment de la droite
joignant gB à gC.
).
Cependant, ce dernier étant ouvert, il contient un plus grand segment de la droite
joignant gB à gC.
Proposition 3.5 La forme bilinéaire gt = (1 - t)gB + tgC est un produit scalaire de
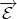 si et seulement si t
si et seulement si t 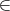 ] - 1∕φ,φ[, où
] - 1∕φ,φ[, où
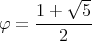
est le nombre d’or.
Preuve. En utilisant les formules (2), (3) et (4), nous voyons immédiatement que
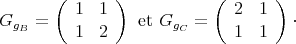
Par conséquent
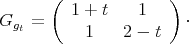
Cette matrice représente un produit scalaire si et seulement si 1 + t > 0 et det Ggt > 0. Cette dernière condition s’écrit t2 - t - 1 < 0. Elle signifie que t est strictement compris entre les racines de l’équation t2 -t- 1 = 0, qui sont -1∕φ et φ. Comme -1∕φ > -1, la propriété est démontrée.
Vu les formules (4), on voit que, dans ( ,gt), le triangle Δ est obtus en B si
t < 0 et en C si t > 1.
,gt), le triangle Δ est obtus en B si
t < 0 et en C si t > 1.
Proposition 3.6 Le lieu de l’orthocentre de Δ lorsque t décrit ]-1∕φ,φ[ est une branche d’hyperbole. Cette hyperbole admet les directions de BC et de la médiane AA′ de Δ comme directions conjuguées(3). Son centre est le point
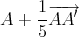
et elle coupe AA′ en A et en
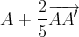
Elle passe par B et par C.
Preuve. En remplaçant p,q,r par les valeurs 1 + t, 2 - t, 1 dans l’expression des coordonnées barycentriques de l’orthocentre, on obtient une description paramétrique du lieu. En passant au repère d’origine A et de base (
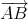 ,
,
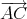 ),
on en déduit des équations paramétriques cartésiennes :
),
on en déduit des équations paramétriques cartésiennes :
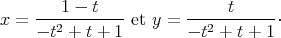
L’élimination est facile et conduit à l’équation cartésienne
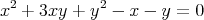
qu’on analyse facilement.